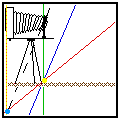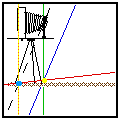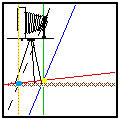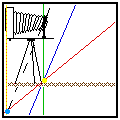
The Hinge Rule and the Scheimpflug Rule together determine how the view
camera focuses. Both rules must be obeyed. The amount and direction of lens
tilt determines where the Hinge Line is. Any movement of the camera back
towards or away from the lens, working through the Scheimpflug Rule, causes
the plane of sharp focus to rotate about the Hinge Line. A PDF-format article
and five short QuickTime movies are available here to illustrate the combined
action of the two rules. There are some spreadsheets
available here also which may help in establishing a consistent standard
of sharpness when one is using a number of different lenses. And there is
a comment on what Harold calls the "Back-to-Front"
method of view camera focus.
[To view these you may obtain Apple's QuickTime and a QuickTime Movie Player
for Windows in 16
bit (QuickTime 2.1 for Windows 3.1) and 32
bit form (QuickTime for Windows 95 and later) from Apple's ftp sites.
For Macs you probably only need the MoviePlayer 2.5, but I'm not sure where
to get it these days. QuickTime for Mac can be downloaded here,
though registration is required. Alternatively, you can use Acrobat Reader
- see next paragraph.] QuickTime MoviePlayer 2.5 actually works better than
later versions because it can be set to "Loop Back and Forth"
and hence play the file continuously.
The article entitled Principles of View Camera Focus
(45k) is available in Adobe Acrobat PDF format. In order to see the figures
become animated on screen one must also download all five of the QuickTime
movies mentioned in the next four paragraphs and place them in the same
folder or directory as the PDF file. Of course, you will also need Adobe Acrobat Reader
to view and/or print the article. (You do not need the movie files in order
to view and print the article, just to see the figures become animated.)
It has been found that Reader 2.1 may not be compatible with the latest
versions of QuickTime. The PDF document can still be read, and the movies
themselves still work fine when viewed with MoviePlayer (which comes with
QuickTime). We found, however, that the animated figures in Principles
of View Camera Focus would not activate automatically upon clicking
on them with Acrobat 2.1 and 32-bit QuickTime under Windows 95, although
Acrobat 3 was OK. On a Power Mac with QuickTime 2.5 installed, neither version
of Acrobat would activate the figures, but the situation was remedied by
putting "QuickTimeTMPowerPlug" (part of QuickTime 2.1) back in
the Extensions folder after installing QuickTime 2.5.
The easiest way to understand the Hinge Rule is to note that the amount
and direction of lens tilt determines where the Hinge Line is. Any movement
of the camera back towards or away from the lens causes the plane of sharp
focus to rotate about the Hinge Line. It's a bit hard to describe in words,
or even in still pictures. But if your software will display QuickTime movies,
download the QuickTime movie file ViewCam.mov
(about 25k). If your movie player permits, tell it to "Loop back and
forth". "Play every frame" is also useful, if provided. If
not, try moving the slider with your mouse to see what's happening in detail.
You should see a) the Hinge Line (yellow dot) staying in one place, b) the
camera back and Film Plane (orange line) moving along the view camera bed,
c) The Scheimpflug line (light blue dot) moving along the Lens Plane (broken
black line) and d) the plane of sharp focus (red line) moving so as to obey
both the Hinge Rule and the Scheimpflug Rule simultaneously. Here's a pre-view:

A Shockwave Flash 2 version of the ViewCam movie is also available. You can view it on a separate page here with Netscape 3 or Internet Explorer 3 (or greater) provided you have Macromedia's Shockwave Flash 'Plug-in'. The Shockwave Flash 2 movie ViewCam.swf is smaller (10k) than the QuickTime version (25k), and shows better detail. This file can also be downloaded and viewed off-line with the Shockwave Flash Player appropriate for your computer.
A second movie, ViewCam2.mov (31k), shows
what happens if the camera back stays still, but the lens is tilted forwards
about an axis through the lens. In this case both the Hinge Line and the
Scheimpflug Line move up and down along the Parallel-to-Film lens plane
and the Film Plane, causing a somewhat complex movement of the plane of
sharp focus (red line). What you see here is representative only when the
camera is initially focused on something relatively close. If the camera
is initially focused near infinity, the plane of sharp focus rotates very
rapidly towards a near-horizontal position far below the camera and then
moves slowly upwards, drawing closer to the camera. ViewCam3.mov
(42k) shows what happens when the front tilt axis lies at the camera base
instead of at the lens axis. The action is similar to the previous case,
but the plane of sharp focus is somewhat higher for any particular amount
of lens tilt.
ViewCam4.mov (34k) illustrates what happens as
one tilts the back of a camera fitted with a back tilt axis that lies about
where the lens axis (for an un-tilted lens) passes through the film. In
this case the lens to film distance at that point does not change, and so
that point on the film is always focused at the same distance. The plane
of sharp focus is thereby constrained to rotate about the intersection of
the lens axis and the original (no back or lens tilt) plane of sharp focus.
As we said, it's easier to illustrate with a moving picture. This is the
simplest and easiest to understand example. And, indeed, one does not need
to use the hinge rule here at all, but is is still obeyed.
ViewCam5.mov (40k) illustrates what happens if
the back is hinged so that the back tilt axis is near the base of the camera.
This geometry caused the plane of sharp focus to rotate about an axis that
is in the original plane of sharp focus (for no back tilt) but somewhat
above the camera.
A second version of the Principles of View Camera Focus may be useful for those who have Acrobat Reader 6 or the full version of Acrobat 5. VuCamTxt+.pdf (140k) is the same basic PDF file, but the movie files are included automatically as attachments. When this file is opened in Acrobat 5 or Acrobat Reader 6 small 'drawing pin' symbols appear beside the word "Movie!" next to each animated diagram. If one double-clicks on one of these symbols, a dialog box opens warning you that this might be a virus but nevertheless offering to open the movie file. If one then clicks "Open", the movie should appear in a separate small QuickTime window. The quality of the illustration is a little better than when the movies are opened within Acrobat. Alternatively, using the Document/Attachments menu item in Acrobat Reader 6, the movie files can be "exported" and hence used normally - if they are placed in the same folder as the PDF file itself. It's still not exactly convenient, but it works. (I tried embedding the movies right in the PDF file using Acrobat 6, but the results are worse than doing it 'the old way': no opportunity to 'Loop Back and Forth', no controller bar to manipulate the animation manually, and poor graphic quality.)
Things related to QuickTime and Acrobat keep changing! As of March 2010 I have added new versions of the movie files and the VuCamTxt PDF file. The zipped archive file "VCmovies.zip" contains the files VuCamTxtLBF.pdf, ViewCam1LBF.mov, ViewCam2LBF.mov etc. through ViewCam5LBF.mov. The movie (.mov) files should now loop back and forth properly with current versions of QuickTime - at least until they are interrupted - and the VuCamTxtLBF.pdf file will open them from Acrobat - provided all these six files are in the same folder. (I again tried embedding the movies in the PDF file itself, but things don't work properly if I do that.) When playing the movies from the PDF document you may need to indicate that you trust the document (depending upon which version of Acrobat Reader or Adobe Reader you are using). I have had difficulty producing versions of the movies that will play properly on an iPod or iPhone except, of course, for the GIF version used above on this page. I did create a larger GIF version, VCGM.gif, which won't play on my (older) iPod Touch But it DOES Play either as an e-mail attachment or a graphic in web page on an iPad! It will not play, however, as a "photo" and it will not be recognized as a "movie" by iTunes, an iPod or an iPad. Here's a version of the first movie (ViewCam1iP.mov) that should loop back and forth six times before closing on an iPod or iPhone. It cannot be loded onto an iPhone or iPod Touch as is; the extension must be changed from .mov to .m4v. That is, download the file to your computer, change the "o" to a "4" in the extension, and then move it into the iTunes Movie window. (The price of "progress": the file is 2.1 MB in size! Compare this to the original .mov file that is 25k in size and runs for ever!) The file ViewCam1iP.mov will play in an iPod or iPhone's web browser fine as is, however. It's just to load it as a stored movie that one needs to change the extension.
View camera depth of field is described briefly on this page. The page also provides a link to Larry Fratkin's on-line view camera depth of field calculator.
Based on discussions with a few readers, I've tried to develop a couple of simple downloadable spreadsheets.
The first spreadsheet is intended to let people develop a table of hyperfocal distances for a set of lenses to be used with a single film format. The almost universal standard used in conventional depth of field calculations is to set the maximum allowable diameter for the circle of confusion to the lens focal length, f, divided by 1500. That's fine when the lens is a 'normal' focal length for the format, but what should one do when using other than normal lenses? Well, instead of f/1500, we really should be using something like F/Q where F is the diagonal measure of the film format, and where Q is a Quality factor. Increasing the value of Q corresponds to demanding a sharper image - but also decreasing the depth of field deemed acceptable. When using a normal lens along with the traditional measure of acceptable image quality, F/Q = f/1500. But using F and Q allows us to standardize image quality standards across a variety of lens focal lengths, and to adjust the desired image quality standard to suit the application. For a 16 by 20 inch print intended to be viewed from close up, one might wish to use Q = 5000. On the other hand, an image intended to occupy only 2 by 3 inches in a newspaper or on a web page may require a value of Q no greater than 300.
The spreadsheet file "HYFOCALD.XLS" permits the user to enter the dimensions of the format in use - either in millimeters or in inches. Simply ensure that there is a "1" under the unit of measure chosen and either a "0" or nothing under the unit not being used. The spreadsheet then calculates the diagonal dimension of the format and divides it by the value of the Quality factor, Q, entered to obtain the diameter, "a", of the largest permissible circle of confusion. Up to six lens focal lengths can be entered, again either in millimeters or in inches (using the same method to specify units as for the format dimensions). The spreadsheet then calculates the actual f/a for each lens and the hyperfocal distances for f-stops (apertures) from f/1 to f/360. The hyperfocal distances can be expressed in millimeters, centimeters, meters, inches, feet or yards. The values of f/a will be of use when using the depth of field tables for tilted lenses contained in FOCUSING the VIEW CAMERA.
The file "LENSTILT.XLS" lets one calculate a table relating the required lens tilt (in degrees) for a variety of J-distances (shown in both meters and feet) and for up to six lens focal lengths at a time. Focal length can be specified in either millimeters or inches using the same method as for the hyperfocal distance spreadsheet: put a "1" opposite the unit being used and either a "0" or a blank opposite the unit not being used. The units are specified separately for each focal length. It is normal to see an error message for combinations of focal length and J-distance where J is less than f: a lens can't focus on anything less than one focal length from it!
Experienced spreadsheet users will be able to extend the spreadsheets to include more than six focal lengths and/or special f-stops, J-distances or whatever.
The spreadsheets were originally prepared using Microsoft Excel, saving the files in Excel 2.2 (.xls) format. The files seemed to work fine for early versions of Excel (Mac) 2.2 and later, as well as Excel 6 for PC and Quattro Pro 8 for PC. In limited cross-platform testing the later Excel 97 format seems to be more reliable, especially for later versions of Excel. The files have thus been converted to this format. The spreadsheet "LENSTILT.XLS" was corrected in early 2016, as the distance conversion from meters to feet was off by about 9%.
The downloadable file "TABLESX.ZIP" (about 22k) is an archive containing three files: "TABLESX.TXT" which is a repeat of this description of the other two files: "HYFOCALD.XLS" and "LENSTILT.XLS". The latter two files are each less than 28k when expanded. The applications Zip-It (PC or Mac) and Stuffit Expander (PC or Mac) can be used to extract the three files from the archive.
The movie files and spreadsheets (or printed versions thereof) are copyright
Harold M. Merklinger of Halifax, Nova Scotia, Canada. With appropriate attribution,
either to "Harold M. Merklinger" or to "http://www.trenholm.org/hmmerk/",
personal or not-for-profit use may be made of these materials. That is,
providing individuals or organizations acknowledge the source of the information
and do not charge for its use or distribution, they may copy and use the
materials provided. Without the express permission of the author, the material
may not be used in or included with printed or formatted-for-computer records
offered for sale. Individual photographers, professional or amateur, are
free to make personal use of this information in their work. Information
on how to contact the author is provided at How
to get these books.
Some Sinar and perhaps other view cameras advertise a method for finding
the amout of lens tilt needed by using the camera back. The suggection is
that it's easier to find the tilt or swing required at the camera back (a
true statement) so one should then be able to transfer that swing or tilt
to the front standard and reset the back to it's original position. Sounds
reasonable, and Harold even mentioned it as a possibility at the end of
the Addendum to FOCUSING the VIEW CAMERA. But, the sad truth is,
the method only works correctly for certain conditions. For close-up situations,
such as product photography, this method over-estimates the amount of tilt
or swing needed. Some people use an iterative method: applying the method
several times in succession (transfer tilt and swing to the front standard,
reset back to original position, tilt or swing back again to find new angles
that put everything in focus, then apply those angles as corrections to
the front, reset the back...etc.) until satisfactory focus is achieved.
There are conditions, however, (typically close-up situations) where repeated
application of the method will not converge to the right answer.
Harold has produced a correction table for photographers using the 'back-to-fornt'
method. To use the table, first use the back as per the original method
to find angles at the back that do the job. Then estimate either the lens-to
film distance (A') along the lens axis, or the image magnification, M. Find
the back angle in the left-hand column, and then read across under the column
for the value of A'/f or M to find the corrected angle to be applied to
the front (lens) movements. (The symbol f, of course, represents the lens
focal length.) Set the lens to these corrected angles, and re-set to back
to its original position.
The correction table can be downloaded in Adobe Acrobat PDF format here (6.5k).
On 2 Mar 97 the correction table was revised to correct for an error
when the initial back angle is greater than 15 degrees. Thanks to Bob Wheeler
for pointing out the problem!
Return to HM Books Table of Contents.
Return to Recent Additions on main page.
Return to View Camera Focus on main page.
More articles on Focus and Depth of Field.